Pochi giorni fa Ryan North, famoso autore canadese di fumetti e programmatore, ha esordito sulla sua pagina Twitter annunciando d’aver scoperto l’equazione matematica del logo di Batman. Avete presente il pipistrello nero su sfondo ellittico tipicamente giallo? Bene. La notizia è stata ripresa anche da Gizmodo USA tramite Mat Honan che da buon scettico ha chiesto ai suoi lettori di verificarla. Ad oggi ancora nessuno si era cimentato nella sua verifica e il perché è presto detto: l’equazione è terribilmente lunga e complessa.
Eccola qui, esattamente come è stata riportata dal suo scopritore.
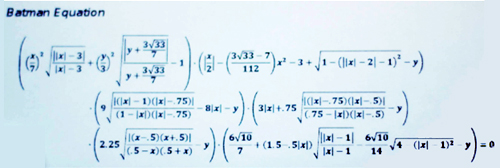
Come molti di voi avranno certamente intuito, si tratta della moltiplicazione di 6 termini complessi, uguagliata a 0. Secondo Ryan North, quindi, rappresentando questa equazione in un grafico cartesiano bidimensionale (coppie di punti x e y) si otterrebbe il famoso logo di Batman.
Il primo passo verso la rappresentazione grafica di una qualsiasi equazione matematica, di qualsivoglia numero di variabili, è la sua conversione in un formato leggibile per un software di calcolo.
La notazione che si suole utilizzare nelle applicazioni scientifiche si chiama infissa. In questo tipo di notazione il simbolo dell’operazione, detto operatore, si scrive tra gli operandi su cui esso agisce. Si tratta della notazione più diffusa, sebbene ne esistano di altre (postfissa e prefissa) ampiamente supportate dai più importanti linguaggi di programmazione. A titolo di esempio: se volessimo sommare 3 e 5, e moltiplicare il risultato per 2 avremmo le seguenti possibili formulazioni (a meno di varianti): - infissa: (3 + 5) * 2
- postfissa (o polacca): 3 5 + 2 *
- prefissa: * 2 + 3 5
Torniamo alla nostra equazione. Per semplicità ho riscritto manualmente in notazione infissa un termine alla volta, utilizzando:
- il simbolo ^ per indicare l’elevamento a potenza;
- la funzione sqrt(_) per indicare la radice quadrata;
- la funzione abs(_) per indicare il valore assoluto.
Si tratta di simboli e nomi di funzioni accettate dalla maggior parte dei software di calcolo e dei linguaggi di programmazione. E’ opportuno notare che nella notazione infissa è indispensabile l’uso delle parentesi al fine di enunciare senza ambiguità l’ordine di applicazione dei vari operatori. Procedendo alla scrittura dei diversi termini in notazione infissa, si ottengono le formulazioni che seguono.
Termine 1:
(((x/7)^2)*(sqrt(abs(abs(x)-3)/(abs(x)-3)))+((y/3)^2)*(sqrt((abs(y+((3*sqrt(33))/7)))/(y+((3*sqrt(33))/7))))-1)
Termine 2:
((abs(x/2))-(((((3*sqrt(33))-7)/112))*x^2)-3+(sqrt(1-(abs(abs(x)-2)-1)^2))-y)
Termine 3:
(9*(sqrt((abs((abs(x)-1)*(abs(x)-0.75)))/((1-abs(x))*(abs(x)-0.75))))-(8*abs(x))-y)
Termine 4:
((3*abs(x))+0.75*(sqrt((abs((abs(x)-0.75)*(abs(x)-0.5)))/((0.75-abs(x))*(abs(x)-0.5))))-y)
Termine 5:
(2.25*(sqrt((abs((x-0.5)*(x+0.5)))/((0.5-x)*(0.5+x))))-y)
Termine 6:
((((6*sqrt(10))/7)+(1.5-(0.5*abs(x)))*(sqrt((abs(abs(x)-1))/(abs(x)-1)))-((6*sqrt(10))/(14))*(sqrt(4-(abs(x)-1)^2)))-y)
Le espressioni sono ora scritte in un linguaggio comprensibile all’elaboratore. Ora è necessario ricostruire l’equazione principale ponendo i vari termini in moltiplicazione tra loro e uguagliando tutto a 0.
Ecco qui l’equazione di Ryan North:
((((x/7)^2)*(sqrt(abs(abs(x)-3)/(abs(x)-3)))+((y/3)^2)*(sqrt((abs(y+((3*sqrt(33))/7)))/(y+((3*sqrt(33))/7))))-1) * ((abs(x/2))-(((((3*sqrt(33))-7)/112))*x^2)-3+(sqrt(1-(abs(abs(x)-2)-1)^2))-y) * (9*(sqrt((abs((abs(x)-1)*(abs(x)-0.75)))/((1-abs(x))*(abs(x)-0.75))))-(8*abs(x))-y) * ((3*abs(x))+0.75*(sqrt((abs((abs(x)-0.75)*(abs(x)-0.5)))/((0.75-abs(x))*(abs(x)-0.5))))-y) * (2.25*(sqrt((abs((x-0.5)*(x+0.5)))/((0.5-x)*(0.5+x))))-y) * ((((6*sqrt(10))/7)+(1.5-(0.5*abs(x)))*(sqrt((abs(abs(x)-1))/(abs(x)-1)))-((6*sqrt(10))/(14))*(sqrt(4-(abs(x)-1)^2)))-y))=0
Utilizzando un qualsiasi software per la rappresentazione di equazioni (in questo caso Texas Instruments Derive 6), si ottiene una piccola sorpresa (molti di voi l’avranno intuito subito): l’operazione di rappresentazione grafica non visualizza un bel nulla. Come mai? Cerchiamo di capirlo insieme.
L’errore di Ryan North è stato quello di porre in moltiplicazione tra loro tutti i singoli termini. Riflettendo sulla geometria del logo di Batman si nota subito che si tratta dell’unione di singoli grafici. Infatti, se visualizziamo le 6 equazioni costruite partendo da ciascun termine (uguagliandolo a 0) otterremo porzioni del logo, che visualizzate contemporaneamente sullo stesso grafico cartesiano rappresentano il logo che noi tutti conosciamo.
Di seguito riporto la rappresentazione grafica dei singoli termini.
Termine 1.
Termine 2.
Termine 3.
_______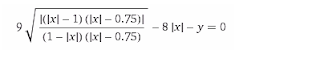
Termine 4.
Termine 5.
Termine 6.
E per finire: ecco qui il logo completo!
L'autore:
Michele Filannino è uno studente di dottorato in Informatica presso il Centre for Doctoral Training dell'Università di Manchester.
Lo scorso anno ha vinto il concorso per giovani ricercatori promosso da Telecom Italia: Working Capital. Nel tempo libero scrive per Melablog.it e per il mensile di tecnologia T3. Ama la matematica ed ogni sua applicazione pratica.

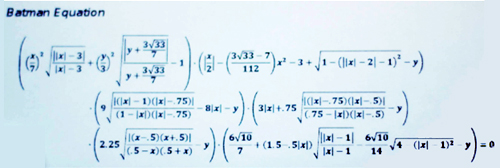


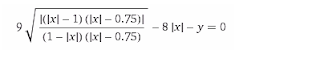









Post a Comment